[시계열] 시계열 데이터, 시계열 데이터 성질, 시계열 데이터의 EDA
1. 시계열 데이터란?
시계열 데이터란 무엇인가?
일정 시간 간격으로 배치된 데이터들의 수열
시계열 분석이란?
시간 순서대로 정렬된 데이터에서 의미 있는 요약과 통계정보를 추출하기 위한 노력
→ 예측하거나 과거의 행동을 진단하는 과정을 포함
현재 시점 t=0
t1 t2 t3.. → 과거
t+1, t+2, t+3… → 미래
데이터 관련 라이브러리 복기
numpy array vs python list
| numpy array | python list |
| 하나의 데이터 타입만 배열에 넣을 수 있음 | 여러 타입들을 배열에 넣을 수 있음 |
| 값들이 저장 | 주소들이 저장 |
| 속도 빠름 | 속도 느림 |
속도 면에서 더 활용도가 높은 numpy를 사용한다.
numpy는 list에 비해 유연성을 부족하지만 연산 속도에 있어 우수
NUMPY
numpy 호출 및 numpy array 생성
import numpy as np
a = np.array([1,2,3])
b = np.array([1,2,3])
Concatenate를 통해 합치기
np.concatenate((a,b))
슬라이싱과 인덱싱
data = np.array([1,2,3])
data[1] # 2
data[0:2] # array([1,2])
data[1:] # array([2,3])
data[-2:] # array([2,3])
numpy연산
data.max() # 3.0
data.min() # 1.0
data.sum() # 6.0
PANDAS
pandas dataframe 은 여러 series(numpy)의 합으로 이루어져 있어 각 컬럼마다 다른 데이터 타입 사용이 가능하다.
즉, 각 컬럼들은 서로 다른 시리즈를 가지고 있기 때문에 다른 데이터 타입 사용이 가능한 것.
dates = pd.date_range("20130101", periods = 6) # periods는 20130101을 포함하여 총 6개의 날짜(년월일) index를 생성
print(dates)
DatetimeIndex(['2013-01-01', '2013-01-02', '2013-01-03', '2013-01-04', '2013-01-05', '2013-01-06'],
dtype='datetime64[ns]', freq='D')
df = pd.DataFrame(np.random.randn(6,4), index = dates, columns = list("ABCD")) # randn은 가우시안 표준 정규분포에서 난수 행렬을 랜덤으로 생성
print(df)
| A | B | C | D | |
| 2013-01-01 | -2.074355 | 0.584191 | -0.734990 | 0.802262 |
| 2013-01-02 | -1.040916 | -1.405000 | 3.220741 | -0.678945 |
| 2013-01-03 | 0.558022 | 0.227992 | -0.611678 | 1.169479 |
| 2013-01-04 | -0.586666 | 0.856881 | 0.349504 | 2.110637 |
| 2013-01-05 | 0.483005 | -0.672247 | -1.525298 | -1.194655 |
| 2013-01-06 | -0.591307 | -2.309199 | -1.927902 | 0.419217 |
index, column 추출
df.index
df.columns
loc, iloc
| label을 넣어 불러옴 | 정수를 넣어 불러오기 |
| start, end포함 | end는 제외 |
시계열 데이터 둘러보기
의료, 금융, 리테일, 그 외
2. 시계열 데이터의 성질

시계열 데이터의 기본 성질

기본 성질별로 시계열을 분해해 보면 어떻게 될까?
original_ts = trend + seasonal + residual
- observed : 원본 데이터
- trend: 확정적 or 확률적
- seasonal: 반복되는 패턴
- random(=residual): 잔차라고도 불리며, trend와 seasonal을 제거한 나머지 요소. 여기서는 더 이상 뽑아낼 수 있는 시계열 기본 성질이 없어야 함. 설명되지 않는 무작위 요소.
예측할 수 있는 것과 없는 것
시계열의 특징이 관측된 시간과 무관하지 않다면, 시간에 따라 특징이 변한다고 볼 수 있다.
현재 시간 t
과거 t-1, t-2, t-3 ..
미래: t+1, t+2, t+3 …
t-1, t-2, t-3까지 관측되었던 시계열 특징이 t+1, t+2, t+3와 동일하지 않을 수 있다.
❓과거 시점을 관측하여 학습된 모델을 미래 시점에 적용하는 것이 맞을까?
그렇기에 정상성이 필요하다.🚀
정상성(Stationarity)은 무엇일까?
시간에 상관없이 일정하다는 강한 가정을 함으로써 추정을 더 강하게 하는 것.
정상성의 종류 - 강정상성과 약정상성
- 강정상성
모든 순간이 시간과 무관하게 일정한 시계열
but, 우리가 마주하는 데이터는 noise가 포함되어 있기도 하고, 다양한 원천에서부터 데이터를 받기 때문에 강정상성을 만족하는 시계열 데이터는 찾기 어려움.
- 약정상성 -> 대부분의 데이터
약정상성을 띠는 시계열 데이터는 어느 시점에 관측해도 확률 과정의 성질( 분산이나 기댓값) 이 변하지 않는다.

정상성이 왜 필요할까?
🔎 왜 "정상성(stationarity)"이 중요한가?
시계열의 예측 가능성은 “과거의 패턴이 미래에도 유지된다”는 가정에서 출발한다.
그런데 시간이 지남에 따라 시계열의 통계적 성질이 변한다면,
→ 과거 데이터로 학습한 모델은 미래 데이터를 잘 예측할 수 없다.
👉그래서 등장하는 개념이 바로 정상성🚀
정상 과정 stationary process
정상성을 띠는 확률 과정이 바로 정상 과정
정상 과정은 어떤 특징을 지니고 있을까?
- 반복되는 패턴
- 일정한 추세
- 일정한 분산
- 계절성도 보이지 않음
약정상성인지 아닌지 확인하는 방법
- KPSS 검정
- ADF 검정
KPSS
귀무가설: 시계열 과정이 정상적이다.
대립가설: 시계열 과정이 비정상적이다.
from statsmodels.tsa.stattools import kpss
kpss(data)
kpss_stat, p-value, lags, crit 네 가지를 반환
→ p-value가 가장 직관적으로 해석 가능
귀무가설 하에서 관측된 결과보다 극단적인 결과가 나올 확률을 0부터 1까지로 표현하고, 0에 가까울수록 귀무가설이 데이터를 잘 설명하지 못한다고 표현.
귀무가설을 기각(=대립가설을 채택) 하기 위한 기준을 유의 수준이라고 부르고, 일반적으로 0.05와 0.01을, 신뢰 수준은 1-신뢰도를 사용한다.
# Kpss 불러오기
from statsmodels.tsa.stattools import kpss
# 시계열 테스트 데이터
time_series_data_test = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# KPSS 검정 수행
kpss_outputs = kpss(time_series_data_test)
# 검정 결과 출력
print('KPSS test 결과 : ')
print('--'*15)
print('KPSS Statistic:', kpss_outputs[0])
print('p-value:', kpss_outputs[1])
KPSS Test 결과 :
------------------------------
KPSS Statistic: 0.5941176470588235
p-value: 0.023171122994652404
ADF
귀무가설: 시계열에 단위근이 존재한다. (= 비정상 시계열)
대립가설: 시계열이 정상성을 만족한다.
from statsmodels.tsa.stattools import adfuller
adfuller(data)
adf, p-value, usedlag, nobs, critical values 등을 반환
→ p-value가 가장 직관적으로 해석 가능
# adfuller 불러오기
from statsmodels.tsa.stattools import adfuller
# 시계열 테스트 데이터
time_series_data_test = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# ADF 검정 수행
adf_outputs = adfuller(time_series_data_test)
# 검정 결과 출력
print('ADF Test 결과 : ')
print('--'*15)
print('ADF Statistic:', adf_outputs[0])
print('p-value:', adf_outputs[1])
ADF Test 결과 :
------------------------------
ADF Statistic: 0.0
p-value: 0.958532086060056
KPSS 검정과 ADF 검정은 어떤 경우에 차이가 나는가?
deterministic trend(=확정적 추세)가 존재하는 경우 차이가 발생
kpss는 기본적으로 around the mean에 대한 검정을 진행하기에 확정적 추세가 존재하는 경우 adf와 다른 결론을 내릴 수 있음
🔎why? adf는 추세 때문에 비정상으로 판단할 수 있지만, kpss는 추세를 무시하고 평균 주위로 안정적인지를 보려 하기에 정상으로 나올 수 있음 🚀
around the mean 시계열이 일정한 평균값을 중심으로 변동하는지, 즉 수평한 평균을 중심으로 안정적인가를 검정
정상성은 어떻게 만들 수 있을까?
1. 분산을 일정하게
- 로그 변환
import numpy as np
import matplotlib.pyplot as plt
import random
# 시계열 데이터 정의
time_series_data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
time_series_data = [random.randint(1, 100) for _ in range(50)]
# 시계열 데이터 로그변환
time_series_data_log = np.log(time_series_data)
# 로그 변환되지 않은 시계열 데이터 시각화
plt.plot(time_series_data)
plt.show()
# 로그 변환된 시계열 데이터 시각화
plt.plot(time_series_data_log)
plt.show()
2. 평균을 일정하게 만든다.
- 회귀
- 평활
import random
import pandas as pd
## 평활 방법 코드
# 랜덤한 수를 가지고 있는 Pandas 데이터프레임을 생성
df0 = pd.DataFrame({'orig_value': [random.uniform(0, 100) for _ in range(100)]})
df1 = pd.DataFrame({'orig_value': [random.uniform(0, 100) for _ in range(100)]})
df0['smoothed_value'] = df0['orig_value'].rolling(5).mean()
# 잡음이 포함된 시계열 데이터를 시각화
df0.plot(legend=True, title='original')
# 잡음이 제거된 시계열 데이터를 시각화
df0.plot(legend=True, subplots=True, title='smoothed')⇒ 나머지로써 추세와 계절성이 제거된 시계열을 얻을 수 있음
- 차분 = 지금 시점 - 어제 시점 = 변화량
한 번의 차이 : 1차 차분
1차 차분으로 다시 차분 : 2차 차분
데이터의 길이가 길면 여러 번 수행될 수 있지만, 대부분의 경우엔 1차 차분만으로 정상적인 시계열이 만들어지며,
2차 이상 차분을 할 경우 해당 데이터에 적합한 모델의 설명력이 낮아지며 데이터 손실이 커진다.
왜 차분을 해야 할까?
비정상적 시계열은 누적 과정 integrated process
매일매일의 변화율이 쌓여서 주가 형태로 띠는 비정상적 시계열이 된 것이다.
즉, 정상적인 시계열이 쌓여서 비정상 시계열이 된 것이기 때문에 차분을 통해 그 이면의 정상적인 과정을 볼 수 있게 된다.
# 위에서 사용한 잡음이 있는 데이터를 그대로 활용하여 시각화
df1.plot(title='original')
# 차분을 적용하고 시각화
df1['diff_value'] = df1['orig_value'].diff()
df1.plot(legend=True, subplots=True, title='diff')3. 시계열에 특화된 EDA
- line plot : 기본적인 시각화
- histogram : 별다른 의미 얻기 어렵지만 1차 차분한 데이터에 대해서는 특정한 분포를 볼 수 있다.
- scatterplot : 상관관계 확인 가능

두 변수가 별다른 관계가 없다. 두 변수간 양의 상관관계를 가진다. 두 변수간 음의 상관관계를 가진다.
- circular chart : 계절성을 시각화할 때 가끔 유용할 때도 있음. 잘 쓰이지 않음.
ACF(AutoCorrelation Function) PLOT = 자기 상관 함수
자기 상관관계가 유의미하냐 유의미하지 않느냐를 판단하기 위해서 임계값을 넣는다.
임계값을 훨씬 넘는 값에 대해서 유의미한 lag라고 판단하고, 그 lag에 자기 상관 계수가 존재한다고 결론을 내린다.
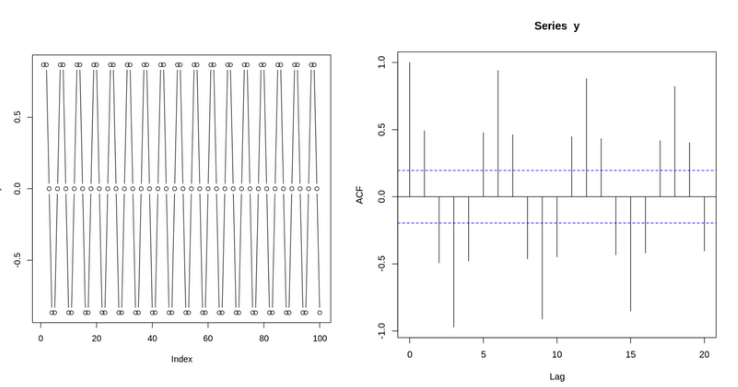
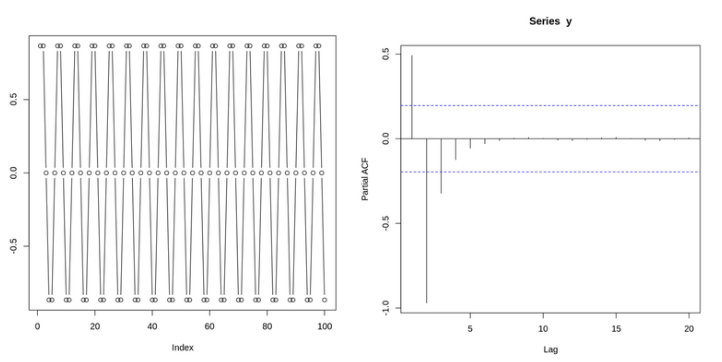
PACF(Partial AutoCorrelation Function) PLOT = 편자기상관 함수
두 지점 사이의 전체 상관관계에서 그 사이 다른 시점의 조건부 상관관계를 뺀 값
쓰는 이유: 불필요한 중복 관계가 제거된다.
ACF와 PACF의 의미적 차이
ACF의 경우 두 시점 간의 상관관계를 계산할 때,
두 시점 사이의 모든 lag에 대한 정보가 들어간다.
하지만 PACF는 오로지 두 시점만의 상관관계만을 계산한다.
(다른 lag는 조건부 상관관계로 제거된다)
🔎why? ACF, PACF로 상관관계를 파악하는 이유?
👉상관관계 분석은 “과거가 미래에 영향을 줄 수 있는가?”를 수치로 확인해서 예측 모델을 설계하려는 목적.
👉예측력이 있는 패턴을 찾아내기 위한 기초 작업인 셈.
Non-stationary 데이터의 ACF 및 PACF
ACF와 PACF는 정상적 데이터 일 때 유용한 정보를 얻을 수 있다.
시계열 EDA에서 체크해야 할 가장 중요한 위험
허위 상관 spurious correlation
유의미해 보인다고 해서 함부로 결론을 내리면 안 된다.