Notice
Recent Posts
Recent Comments
Link
- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 회고
- 함수
- 2주차
- 데이터사이언스
- 회고록
- 빅쿼리
- github
- 모두의연구소
- error
- 개념정리
- 깃허브
- 머신러닝
- 1주차
- AI
- ML
- python
- 데이터
- data
- 부트캠프
- 파이썬문법
- 데이터사이언티스트
- Jupyter Notebook
- 파이썬
- 프로젝트
- sql
- 딕셔너리
- 주피터노트북
- 변수
- bigquery
- 딥러닝
Archives
[ML] 지도학습(회귀) 모델, 하이퍼파라미터 튜닝, 모델 평가 본문
반응형
지도학습 모델 및 모델 평가
1. 지도학습
- 선형회귀
- 릿지 회귀
- 릿지 회귀 alpha 조정
- 라쏘 회귀
- 라쏘 회귀 alpha 조정
- 엘라스틱넷 회귀
- 엘라스틱넷 회귀 alpha, l1_ratio 조정
- 랜덤포레스트 & XGBoost
- 하이퍼 파라미터 튜닝
- GridSearchCV
- RandomizedSearchCV
2. 회귀 모델 평가
- MAE
- MSE
- RMSE
- RMSLE
- R² Score
사용 툴: tldraw
전체 흐름도
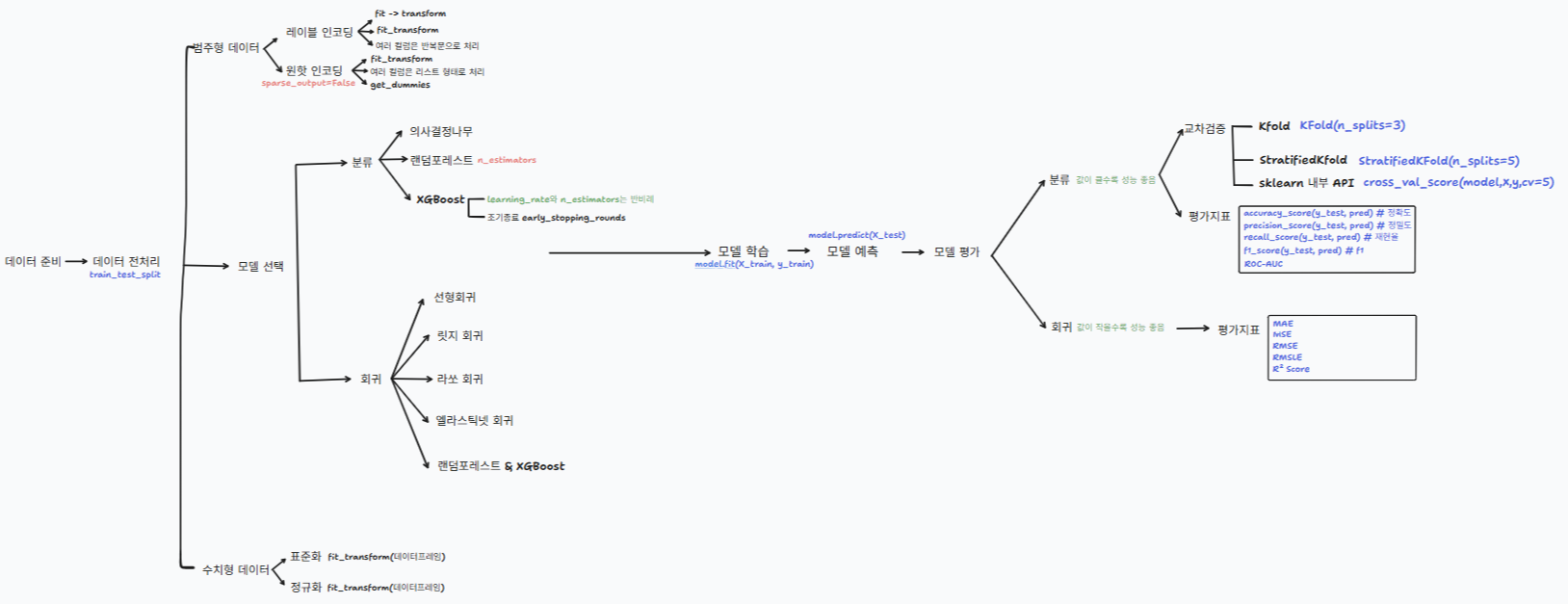
지도학습 모델 및 모델 평가

데이터 불러오기
# 데이터 생성
from sklearn.datasets import load_diabetes # 당뇨병 환자 데이터
def make_dataset():
dataset = load_diabetes()
df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df['target'] = dataset.target
X_train, X_test, y_train, y_test = train_test_split(
df.drop('target', axis=1), df['target'], test_size=0.2, random_state=1004)
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = make_dataset()
X_train.shape, X_test.shape, y_train.shape, y_test.shape
📑 헷갈리는 개념 정리
| X_train | 수학 문제 |
| y_train | 수학 문제 정답 |
| X_test | 새로운 수학 문제 |
| y_test | 새로운 수학 문제 정답 |
👉 train 데이터로 학습하고 test 데이터로 예측하여 나온 결과와 target을 비교하여 모델 성능을 나타낸다. 🚀
지도학습(회귀)
🛠 선형 회귀
# 선형 회귀
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
# 2707.6318521641583
🛠 릿지 회귀
# 릿지 회귀
from sklearn.linear_model import Ridge
model = Ridge() # default alpha=1 이것으로 규제를 조정할 수 있다.
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
# 3522.1191842072662
릿지 회귀는 가중치(회귀 계수)에 패널티를 준다.
L2 규제를 사용해서 모델의 계수가 너무 커지는 걸 막는다.
alpha가 커질수록 계수들이 줄어든다(=규제가 강해진다)
✅ 과적합(Overfitting) 방지 vs. 설명력
- 작은 alpha → 계수가 자유로움 → 모델이 복잡해져서 과적합 위험 증가
- 큰 alpha → 계수가 억제됨 → 모델이 단순해져서 과소적합 가능성
그래서 alpha를 바꿔보며 성능과 계수 변화의 균형을 관찰한다.🔥
# 회귀 계수
# 출력되는 값들은 피처들의 순서다. (age, sex..의 회귀 계수)
model.coef_
# 출력 결과
array([ 31.2934206 , -71.44865465, 267.60596214, 197.36249197,
14.61325736, -13.88423665, -124.64983613, 106.21296724,
221.0684933 , 101.20254637])
# 어떤 변수의 회귀계수인지 판단하기 어려우므로 dataframe으로 변경
coef = pd.DataFrame(data=model.coef_, index=X_train.columns, columns=['alpha1'])
coef
# 출력 결과
alpha1
age 31.293421
sex -71.448655
bmi 267.605962
bp 197.362492
s1 14.613257
s2 -13.884237
s3 -124.649836
s4 106.212967
s5 221.068493
s6 101.202546alpha값 조정하는 코드
# 릿지 회귀 alpha=10으로 조정
from sklearn.linear_model import Ridge
model = Ridge(alpha=10)
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
dataframe으로 만드는 코드
coef['alpha10'] = model.coef_
coef

🛠 라쏘 회귀
# 라쏘 회귀
from sklearn.linear_model import Lasso
model = Lasso() # default alpha 1
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
# 4179.152642946345
alpha값 조정하는 코드
# 라쏘 회귀 alpha=0.05
from sklearn.linear_model import Lasso
model = Lasso(alpha=0.05)
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
# 2703.4583679188177
dataframe으로 만드는 코드
coef = pd.DataFrame(data=model.coef_, index=X_train.columns, columns=['alpha1'])
coef
# 중요하다고 생각되는 피처만 남겨두고 나머지는 0으로 만든다.
# alpha=0.05
coef['alpha0.05'] = model.coef_

🛠 엘라스틱넷 회귀
# 엘라스틱넷 회귀
from sklearn.linear_model import ElasticNet
model = ElasticNet()
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
# 6539.270961171604
alpha와 l1_ratio 파라미터 조정
# 엘라스틱넷 회귀
from sklearn.linear_model import ElasticNet
model = ElasticNet(alpha=0.0001, l1_ratio=0.6) # default l1_ratio 0.5
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred) # 오차숫자는 작을수록 좋음
# 2675.6031657225317
🛠 랜덤포레스트 & XGBoost
=> 분류에서뿐만 아니라 회귀에서도 사용되는 모델
# 랜덤포레스트
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred)
# 3233.3248640449438
# Xgboost
from xgboost import XGBRegressor
model = XGBRegressor()
model.fit(X_train, y_train)
pred = model.predict(X_test)
mean_squared_error(y_test, pred)
# 4265.475533439266
🛠 하이퍼 파라미터 튜닝
# 라이브러리 불러오기
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
# 하이퍼파라미터
params={'learning_rate':[0.07, 0.05],
'max_depth':[3, 5, 7],
'n_estimators':[100, 200],
'subsample':[0.9, 0.8, 0.7]
}
# 데이터셋 로드
def make_dataset2():
dataset = load_diabetes()
df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df['target'] = dataset.target
return df.drop('target', axis=1), df['target']
X, y = make_dataset2()
🛠 GridSearchCV
# GridSearchCV
xgb = XGBRegressor()
grid = GridSearchCV(xgb, params, cv=3, n_jobs=-1)
grid.fit(X, y)
# 최적의 하이퍼파라미터를 찾음
grid.best_params_
# 하이퍼파라미터 튜닝
xgb = XGBRegressor(
learning_rate = 0.05,
max_depth = 3,
n_estimators = 100,
subsample =0.7
)
xgb.fit(X_train, y_train)
pred = xgb.predict(X_test)
mean_squared_error(y_test, pred)
# 3016.599930669008
🛠 RandomizedSearchCV
# Randomized Search
xgb = XGBRegressor()
grid = RandomizedSearchCV(xgb, params, cv=3, n_iter=10, n_jobs=-1)
grid.fit(X, y)
# 최적의 하이퍼파라미터를 찾음
grid.best_params_
# 하이퍼파라미터 튜닝
xgb = XGBRegressor(
learning_rate = 0.05,
max_depth = 3,
n_estimators = 200,
subsample =0.7
)
xgb.fit(X_train, y_train)
pred = xgb.predict(X_test)
mean_squared_error(y_test, pred)
# 3218.7105269306708
모델 평가
🛠 MAE
실제 값과 예측 값의 차이(오차)를 절댓값으로 계산한 평균
- 값이 작을수록 좋음
🛠 MSE
오차를 제곱하여 평균 낸 값
- 값이 작을수록 좋음
🛠 RMSE
MSE의 제곱근
- 값이 작을수록 좋음
🛠 RMSLE
실제 값보다 큰 예측은 작은 예측보다 덜 패널티를 줌
- 값이 작을수록 좋음
🛠 R² SCORE
모델이 전체 변동성 중 얼마나 설명했는지를 나타냄
- 1.0: 완벽한 예측
- 0.0: 평균 수준
- 0보다 작음: 무작위 예측보다 못함
# MAE
from sklearn.metrics import mean_absolute_error
print(f'MAE: ',mean_absolute_error(y_test, pred))
# MSE
from sklearn.metrics import mean_squared_error
print(f'MSE: ',mean_squared_error(y_test, pred))
# RMSE
import numpy as np
print(f'RMSE: ',np.sqrt(mean_squared_error(y_test, pred)))
# RMSLE
from sklearn.metrics import mean_squared_log_error
print(f'RMSLE: ',np.sqrt(mean_squared_log_error(y_test, pred)))
# R^2
from sklearn.metrics import r2_score
print(f'R^2: ',r2_score(y_test, pred))
# 출력 결과
MAE: 46.916792151633274
MSE: 3218.7105269306708
RMSE: 56.73368071023306
RMSLE: 0.43239748906910014
R^2: 0.5084076080010445'Machine Learning' 카테고리의 다른 글
| [시계열] 시계열 데이터, 시계열 데이터 성질, 시계열 데이터의 EDA (5) | 2025.05.22 |
|---|---|
| [ML] 비지도학습 - 군집화(Clustering) (0) | 2025.05.20 |
| [ML] 지도학습(분류) 모델, 하이퍼파라미터 튜닝, 모델 평가 (0) | 2025.05.12 |
| [ML] Machine Learning 머신러닝 과정 정리 (코드로 이해하기) (1) | 2025.05.08 |




